□ EMW 에서 사선으로 들어오는 평면파의 구현
- 사선 평면파의 방향은 구조체의 Coordinate 와 공간 각 을 고려 아래와 같이 표현됩니다.
- 이 경우 EMW Script 예제는 아래와 같습니다.

PlaneWaveExcitation{
## Exciatation distance from device is 0.3 um (60 cells).
## Area of box does not affect the results. (Always full to domain size)
BoxCorner1 = (@<@DEPTH@+BARL+2>@, 0.0, 0.0) # um
BoxCorner2 = (@<@DEPTH@+BARL+2>@, @WIDTH@, @WIDTH@) # um
## The wave with Theta=90 & Phi=180 is perpendicular to device, from X- to X+ direction.
## <Z+ means wave propagates to the Z=A -> Z=B direction (A < B) with constant Y
## Theta -> 80 & Phi=180 has incident angle <Z+ = 10 degree
## Theta -> 100 & Phi=180 has incident angle <Z- = 10 degree
## Theta=90 & Phi -> 170 has incident angle <Y+ = 10 degree
## Theta=90 & Phi -> 190 has incident angle <Y- = 10 degree
Signal = harmonic
Theta = @theta@
Phi = @phi@
Psi = 0
Wavelength = @<1000.*wavelength>@ # nm
Intensity = 0.00002 # W/cm2 & 1 lux = 0.0079 W/m2 & bright sunlight = 120000 lux = 948 W/m2
# Global solar spectrum sunlight => 109880 lux = 1000 W/m2
Nrise = 5 # number of signal periodeds until full power
Delay = 0
}
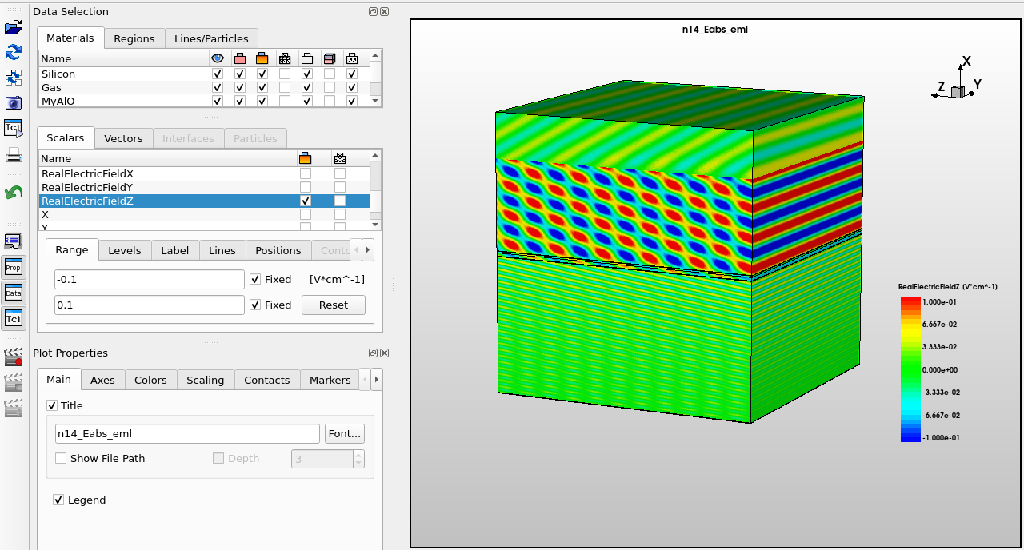
Plot {
Name = "n@node@_Eabs"
Quantity = {AbsElectricField,AbsMagneticField, realelectricfieldx, realelectricfieldy, realelectricfieldz, Region}
FinalPlot = yes
}
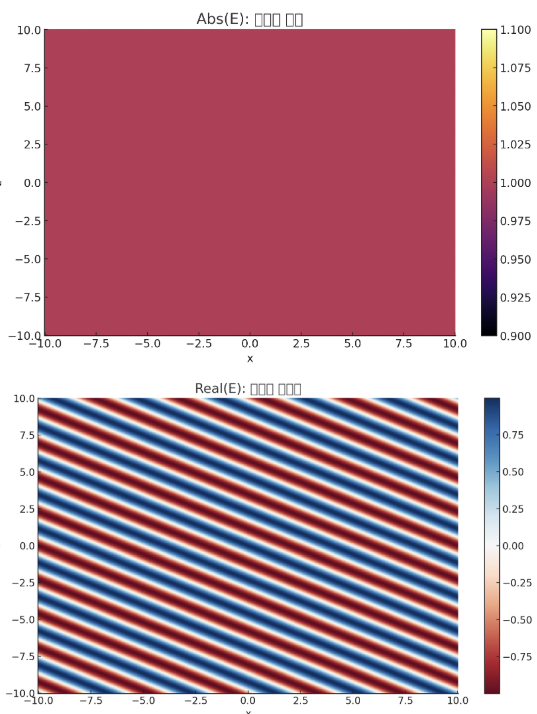
□ Abs(Electric Field): 전기장의 크기(진폭) 표현
- 전기장을 복소수로 표현할 경우, E = E₀·exp(i(k·r - ωt))와 같이 시간과 공간에 따라 진동하는 파동 형태로 나타납니다.
- Abs(E)는 이 복소수 전기장의 절댓값, 즉 크기를 의미하며 다음과 같이 계산됩니다:
|E| = sqrt(Re(E)² + Im(E)²) - 특징:
- 위상 정보가 제거됩니다.
- 시간과 관계없는 상수 진폭 분포만 남습니다.
- 파동이 기울어졌는지 여부는 크기 분포만으로는 잘 드러나지 않음.
- 간섭, 위상 차 같은 정보도 표현되지 않음.
□ Real(Electric Field): 전기장의 실수부 표현
- Re(E) = Re[E₀·exp(i(k·r - ωt))] = E₀·cos(k·r - ωt)
- 실시간 전기장의 진동 형태를 보여줍니다.
- 특징:
- 위상 정보가 보존됨.
- 파동이 진행되는 방향에 따라 기울어진 파면이 명확히 보임.
- 사광 입사 시, 파면이 일정 각도로 기울어져 있는 형태가 나타남.
- 시간 t에 따라 변화하므로, 애니메이션으로 보면 파가 어디서 어디로 진행하는지 시각적으로 파악 가능.
⚠️ 주의사항
- Abs(E)만 보면 빛의 방향성, 간섭, 위상차 등 파동의 중요한 특성을 놓칠 수 있음.
- 사광 입사나 간섭 패턴, 회절 분석 등에서는 항상 Real(E) 또는 복소수 표현 자체를 함께 고려해야 함.
import numpy as np
import matplotlib.pyplot as plt
# 공간 격자 설정
x = np.linspace(-10, 10, 400)
z = np.linspace(-10, 10, 400)
X, Z = np.meshgrid(x, z)
# 파동 파라미터
wavelength = 2.0 # 파장
k = 2 * np.pi / wavelength # 파수
theta_deg = 30 # 입사각 (도)
theta = np.radians(theta_deg) # 라디안으로 변환
# 파벡터 성분 (사광 입사)
kx = k * np.sin(theta)
kz = k * np.cos(theta)
# 시간 설정 (정적 시간 스냅샷)
t = 0
# 복소 전기장 (시간 고정)
E_complex = np.exp(1j * (kx * X + kz * Z - t))
# 크기와 실수부 계산
E_abs = np.abs(E_complex)
E_real = np.real(E_complex)
# 시각화
fig1, ax1 = plt.subplots()
c1 = ax1.pcolormesh(X, Z, E_abs, shading='auto', cmap='inferno')
ax1.set_title("Abs(E): 전기장 크기")
ax1.set_xlabel("x")
ax1.set_ylabel("z")
fig1.colorbar(c1, ax=ax1)
fig2, ax2 = plt.subplots()
c2 = ax2.pcolormesh(X, Z, E_real, shading='auto', cmap='RdBu')
ax2.set_title("Real(E): 전기장 실수부")
ax2.set_xlabel("x")
ax2.set_ylabel("z")
fig2.colorbar(c2, ax=ax2)
plt.tight_layout()
plt.show()'Solution > Optic TCAD' 카테고리의 다른 글
| Tetracell Structure (0) | 2025.12.16 |
|---|---|
| PMI model (0) | 2025.04.02 |
| Optic 구조2 (0) | 2024.05.18 |
| 0.8 um QE test (0) | 2024.01.29 |
| Optic Color Filter n, k Information (1) | 2023.12.19 |